Softwarepraktikum: Numerik mit DUNE

Ansgar Burchardt <ansgar@mathi.uni-heidelberg.de>

DUNE (Distributed and Unified Numerics Environment) ist eine C++-Programmbibliothek zum Lösen von partiellen Differentialgleichungen mittels finiter Elemente, finiter Volumen oder finiter Differenzen. Es wird stark Gebrauch von modernen C++-Programmiertechniken wie Templates gemacht. DUNE ist modular aufgebaut und macht es möglich verschiedene Implementierungen für Gitter, Löser usw. mit einem gemeinsamen Interface zu verwenden. Auch das Rechnen auf Parallelrechnern ist möglich, vorausgesetzt die verwendeten Module unterstützen dies.

Gitter

DUNE bietet ein abstraktes Interface für Gitter. Es gibt verschiedene Implementierungen, etwa SGrid (strukturierte Gitter aus Würfeln, nur für Testzwecke), OneDGrid (adaptives 1D-Gitter), YaspGrid (strukturierte Gitter, unterstützt paralleles Rechnen) und UGGrid (unstrukturierte Gitter in 2- und 3D, basiert auf UG).

Um sich etwas mit dem Gitterinterface vertrat zu machen, habe ich ein Programm zum Berechnen des Integrals einer Funktion auf einem Interal [a,b] geschrieben. Hierbei wurde die Integration von Hand mit Simpsonregel (Trapezregel) implementiert ohne die dazu ebenfalls in DUNE vorhandenen Funktionen zu verwenden. Zusätzlich wurde eine adaptive Gitterverfeinerung implementiert; hierbei wird der Fehler über die Differenz zur als bekannt vorausgesetzten analytischen Lösung berechnet.

Wichtige Punkte:

Erzeugen von (einfachen) Gittern,
Iteration über Zellen,
Umrechnen von lokalen Koordinaten auf dem Referenzelement zu globalen Koordinaten,
Verwenden von Mappern um Daten mit Bezug zu Zellen zu speichern,
adaptive Gitterverfeinerung.

Quellcode:

integration_auf_1d_gitter.cc

Lösung linearer Gleichungssysteme

Beim Lösen partieller Differentialgleichungen spielt die lineare Algebra eine wichtige Rolle. Hierbei unterscheidet DUNE zwischen der in der Problemstellung auftretenden Vektoren und (in der Regel dicht besetzten) Matrixen, die durch FieldVector (FieldMatrix) dargestellt werden, und den bei der Lösung auftretenden Blockvektoren und (in der Regel dünn besetzen) Matrizen, die etwa durch BlockVector (BCRSMatrix) dargestellt werden.

Aufgabe war die Laplace-Gleichung mit Dirichlet-Nullrandbedingungen, also -Δu=0 auf Ω, u=0 auf ∂Ω, in 2D auf dem Gebiet Ω = [0,1]² mittels finiter Differenzen zu lösen. Die im zugehörigen linearen Gleichungssystem auftauchende Matrix wurde durch eine BCRSMatrix< FieldMatrix<double,1,1> > dargestellt und das Gleichungssystem mit verschiedenen Lösern aus der ISTL (Iterative Solver Template Library) gelöst.

Wichtige Punkte:

Darstellung von Matrizen und Vektoren, insbesondere auch von dünn besetzen Matrizen,
Aufruf von Lösern für lineare Gleichungssysteme,
einfaches Benchmarking mit Dune::Timer.

Quellcode:

laplace_mit_finiten_differenzen.cc

Lösung der Laplace-Gleichung mit PDELab

Mit PDELab bietet DUNE eine Bibliothek für die einfache Implementierung von Programmen zur Diskretisierung und Lösung von Systemen partieller Differentialgleichungen. Es werden Mittel zur Erzeugung diskreter Funktionenräume und auf der Methode der gewichteten Residuen basierende Operatoren bereitgestelt, der Anwender muss nur einen lokalen Operator auf dem Referenzelement implementieren.

In diesem Teil des Praktikums sollte das Beispiel 2 aus dem PDELab-Howto so modifiziert werden, dass wie im vorherigen Teil das Laplace-Problem mit Dirichlet-Nullrandbedingungen auf dem Einheitsquadrat gelöst wird. Als Gitter wurde ein Vierecksgitter mit YaspGrid und ein Dreiecksgitter mit UGGrid verwendet.

Wichtige Punkte:

Formulierung von Problemen mit PDELab,
Verwendung von PDELab mit verschiedenen Gittern und Ansatzräumen.

Quellcode:

Selbststrukturierende Systeme

Einige selbststrukturierende Systeme können durch die Reaktions-Diffusions-Systeme beschrieben werden, ein Beispiel hierfür ist die FitzHugh-Nagumon-Reaktion, die durch folgendes Gleichungssystem beschrieben wird:

∂_tu₀ - d₀Δu₀ - f(u₀) + σu₁ = 0 auf Ω,
τ∂_tu₁ - d₁Δu₁ - u₀ + u₁ = 0 auf Ω,
∇u₀·n = ∇u₁·n = 0 auf ∂Ω,
u₀(·,t₀) = U₀(·), u₁(·,t₀) = U₁(·).

Hierbei ist Ω = (0,2)² (oder (0,2)³) und f(u) = λu - u³ - κ.

Das Beispiel 5 aus dem PDELab-Howto löst dieses Problem in 2D mit u_i ∈ Q1 und, nach einer kleinen Änderung im Quelltext, u_i ∈ Q2; hierbei wird der Funktionenraum einmal mit Hilfe von CompositeGridFunctionSpace aus den einzelnen Q1-Räumen bzw. mit PowerGridFunctionSpace aus den Q2-Räumen aufgebaut.

Das Programm wurde modifiziert um unterschiedliche Startwerte U_i(·) zuzulassen, wodurch sich andere Lösungen ergeben. In einem weiteren Schritt wurde als Ansatzraum eine Mischung aus Q1-Funktionen für u₀ und Q2-Funktionen für u₁ gewählt. Im letzten Teil wurde das programm so modifiziert, dass es das Problem mit Q1Q1-Ansatzfunktionen auch im dreidimensionalen Raum lösen kann. Hierbei wurde auch ein Backend gewählt, das es erlaubt die Lösung parallel auf mehreren Rechnern zu berechnen.

Rechnung mit Q1Q1-Ansatzfunktionen

Wichtige Punkte:

Erzeugen zusammengesetzter Funktionenräume mit Dune::PDELab::CompositeGridFunctionSpace und Dune::PDELab::PowerGridFunctionSpace,
einfacher Wechsel zwischen Ansatzräumen,
einfache Parallelisierung durch Verwenden geeigneter Gitter- und Löserimplementierungen.

Quellcode:

Adaptive Gitterverfeinerung

Auf dem Gebiet Ω = { (x,y) : -1 < x < 1, -1 < y < 1 } \ { (x,y) : 0 ≤ x < 1, -1 < y ≤ 0 } wird das Laplace-Problem Δu=0 gelöst. Die Randdaten werden durch die analytische Lösung g(r, φ) = r^(2/3) sin(2/3 φ) vorgegeben.

Die adaptive Gitterverfeinerung von DUNE wurde mit dem in "Numerik partieller Differentialgleichungen" vorgestellten a-posteriori Fehlerschätzer verwendet, und die erreichte Genauigkeit mit globaler Verfeinerung verglichen.

Adaptive Gitterverfeinerung

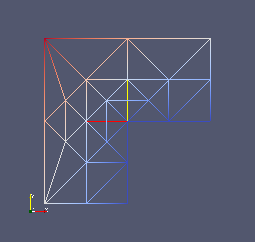
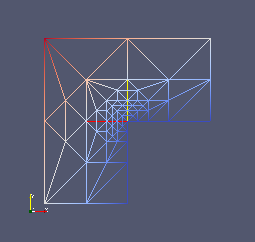
Die adaptive Verfeinerung erkennt die problematische Stelle (0,0) und verfeinert das Gitter dort.

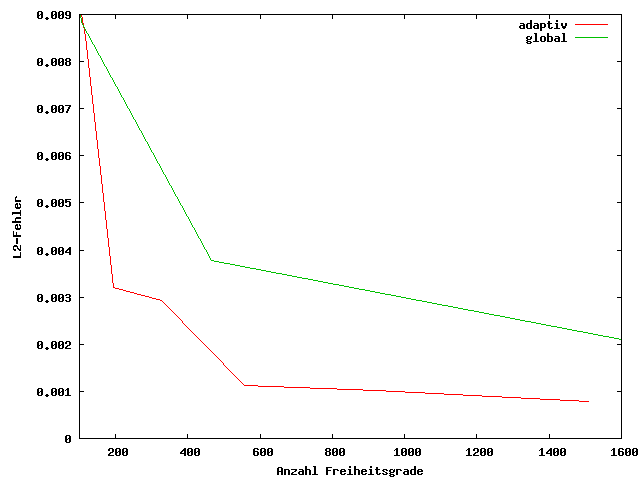
L2-Fehler über Anzahl der Freiheitsgrade

Mit adaptiver Gitterverfeinerung kann bei gleichem Aufwand (gleicher Anzahl Freiheitsgrade) ein merklich geringerer Fehler erreicht werden.

Quellcode:

adapting_grid.cc